
Inhoud
- Zipf's wet uitgelegd
- Eenvoudig experiment
- Zipf's Law in Steam-markten
- Wat kunnen we leren over Steam?
- conclusies
Een tijdje geleden stelde een vriend van mij voor om video's van Vsauces te bekijken over de wet van Zipf, het principe van Pareto en hun mysterieuze verschijningen overal om ons heen. Hier is een kleine teaser om uw aandacht te trekken - 80% van alle mensen woont in 20% van de populairste steden; 80% van alle grond behoort toe aan 20% van de rijkste verhuurders; 80% van alle afval staat in de top 20% van de meest trashiest straten - zoals voorspeld door de wet van Zipf en het Paretos-principe.
Niet genoeg? Welnu, zoals ik gisteren ontdekte, stopt het konijnenhol daar niet ... Vol scepsis, besloot ik om te kijken hoeveel tijd mensen besteden aan het spelen van Steam-spellen ... Wel. 80% van de tijd van mensen wordt besteed aan het spelen van 20% van de populairste games ... Interessant? Nou, lees verder, er is meer aan dit verhaal.
Met een kloksnelheid van meer dan 20 minuten is Vsauces-inspanning geweldig en worden veel van de grote dingen over Zipf uitgelegd, maar hij is erg verlegen om ons het kernmechanisme te tonen waarvan algemeen wordt aangenomen dat het bijdraagt aan de reden waarom Zipf werkt zoals het werkt. Dus voordat we verder gaan, wil ik dat kort uitleggen.
Zipf's wet uitgelegd
Er zijn verschillende conceptuele manieren om de intuïtie achter het 20/80-principe te verklaren. Het beste voorbeeld is naar mijn mening die over maankraters.
Eenvoudig experiment
Dus, stel je voor als je wilt, dat er een onaangeroerde maan is - een perfect glad oppervlak. Stel dat er een aantal asteroïden van willekeurige grootte zijn die willens en wetens tegen de maan slaan. Wanneer de eerste asteroïde landt, verlaat het een krater. Nu raakt er nog eentje geraakt, waardoor er elders een krater achterblijft. Elke krater is een deel van het totale oppervlak, daarom is er een kans dat de volgende willekeurige asteroïde dicht bij een bestaande krater zal slaan en zich ermee verenigen, en een groep vormen. De kans dat een nieuwe asteroïde een bepaalde krater raakt, is dan evenredig met de bestaande grootte van de kraters en asteroïden. Dit betekent dat de volgende willekeurige asteroïde eerder lid wordt van de grootste bestaande groep, waardoor deze nog groter wordt. Een soort cumulatief proces, dat vervolgens een rich-get-richer poor-get-lonelier-mechanisme creëert.
Houd dit in gedachten, want dat wordt verondersteld de algemene verklaring te zijn voor 'waarom' de wet van Zipf met zo'n mysterieuze universaliteit werkt. Het asteroïde voorbeeld is vrij eenvoudig, maar de vraag is wat er zal gebeuren gedurende vele herhalingen
Een beetje verbijsterend?
Wel, ik heb een gif gemaakt om dit eerste punt naar huis te rijden. NB! de grafiek zal later worden besproken, probeer gewoon het experiment voor te stellen.

Als we de werkelijke maan waarnemen, blijkt dat, als de hoeveelheid asteroïden tot grote hoeveelheden toeneemt, de waargenomen kraterdiameters zodanig groeien dat de bovenste 20% van de grootste kraters 80% van het totale oppervlak naderen.
Dus als we naar meer asteroïden gaan, benadert de verspreiding van de meest populaire tot minst populaire groepen een soort van "ideale distributie" met deze eigenschap 20/80 - een Pareto-distributie. Als je de wiskunde doet, blijkt dat (in het algemeen), als de grootste groep de grootte N heeft, de op een na grootste groep rond de grootte N / 2 ligt, de derde N / 3 enzovoort enzovoort. Dit wordt de Zipf's wet genoemd. Het rare is de wet van Zipf en de Pareto-distributie werkt voor een verbijsterende hoeveelheid elementen (asteroïden) en groepen (kraterclusters). Natuurlijk zijn er skews en willekeurige verstoringen, maar de algemene trend is onmiskenbaar.
Ik hoop dat je kunt zien hoe asteroïden die vaker grote kraters raken op de maan, verbinding maken met steden die aantrekkelijker zijn, als er al meer mensen in wonen. Je moet je echter realiseren dat steden ver van de enige "groepen" zijn die zich volgens Zipf gedragen.
Hier zijn enkele voorbeelden van Mark Newmans onderzoek naar Pareto-distributies. NB! De grafieken zijn in log-log-schaal die de hyperbolische vorm van de curven effent, waardoor een bijna lineaire relatie wordt weergegeven.
Initial y = aX ^ (- b)
Logs van beide kanten => log y = log a - b log X
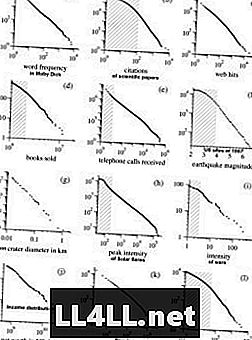
Interessant is dat dezelfde trend ook wordt weergegeven door religieuze sekten ... Het gemeenschappelijke kenmerk van de meeste van deze fenomenen is gewoon deze neiging van 'grote groepen-wordt groter'. Dus de wet van Zipf is persistent in mechanismen, waarbij de voorkeuren van elementen positief verbonden zijn met de groepsgrootte (dus hoe groter de groep, hoe groter de kans dat die groter wordt). Dit is waarom ik groepen graag zie als clusters en elementen als cluster-ers.
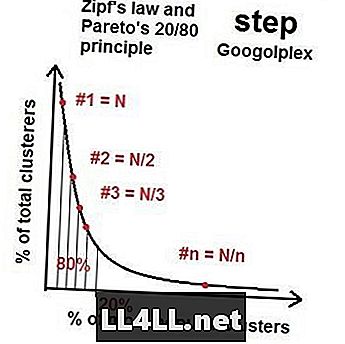
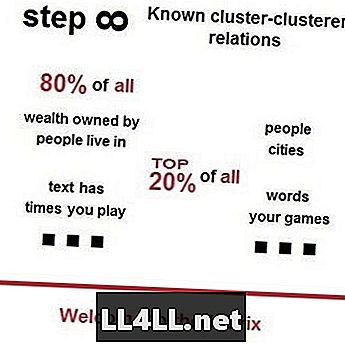
Zipf's Law in Steam-markten
Verdacht van die laatste? Hier is de hoeveelheid tijd die mensen besteden aan de meest populaire spellen op Steam. Gegevens van SteamSpy.
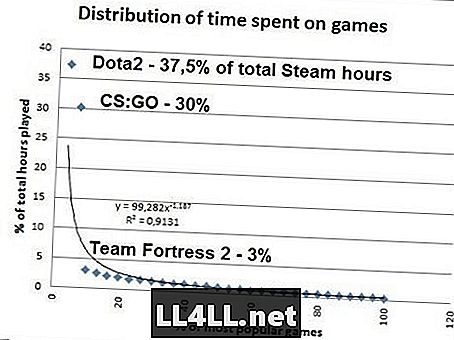
Als je de wiskunde doet, blijkt dat 20% van de meest populaire Steam-spellen 80% van het totale aantal spelen uitmaken, dus het Pareto 20/80-mysterie werkt hier als een charme ... Je moet echter wel opletten dat voor Zipf om waar te zijn, CS: GO moet rekening houden met 37,5% / 2 = 18,8% van de totale tijd in plaats van maar liefst 30%. Maar afgezien van deze uitbijter (STOP AFSPELEN CS: GO), de Zipf-achtige verdeling is duidelijk aanwezig.
Hier is het aantal verkochte exemplaren voor de meest populaire spellen.
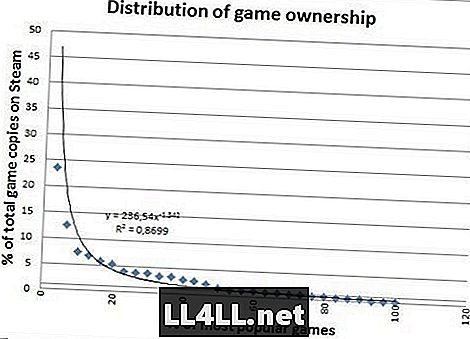
Ziet er veel leuker uit? Verkochte exemplaren hebben geen grote uitbijters, dus het past heel goed, wat een opmerkelijk verschil is. Er is echter iets interessants om uit de verschillen van de laatste twee grafieken te concluderen.
Merk je op hoe de "staart" naar rechts een beetje dik is in de tweede grafiek? Welnu, in eenvoudige bewoordingen, dit vertelt ons dat de "relatief onpopulaire" games eigenlijk best veel populairder zijn dan in de vorige plot.
Het blijkt zelfs dat 20% van de meeste populaire games slechts 60% van de omzet uitmaakt, tegenover 80% van het spel. Interessant? Je weet zeker dat het is.
Wat kunnen we leren over Steam?
Welnu, het feit dat de populariteit van spellen volgt op de distributie van Pareto, leert ons dat er inderdaad een soort positief netwerkeffect is, waardoor spelers games kiezen die al door meer mensen worden gespeeld. Wat het verschil in vetheid van staarten is, is dat Steam-gebruikers veel meer "group-size-blind" zijn, wanneer ze games kopen dan wanneer ze ze spelen.
Denk er eens over - hoe meer mensen games kopen, ongeacht de 'huidige populaire mening', hoe meer de Pareto-distributie wordt afgeplat, omdat het minder waarschijnlijk is dat grote games verder groeien. Als niemand een rattenkont stootte over hoeveel mensen al een spel spelen en de beschikbaarheid van alle spellen hetzelfde was, dan zouden we verwachten dat 20% van de meeste populaire spellen verantwoordelijk is voor ongeveer 50% van de verkoop en speeltijd (bijvoorbeeld uitgaande van individuele voorkeuren normaal verdeeld).
conclusies
Er zijn dus twee factoren die bijdragen aan de Pareto-distributie op Steam-markten - hoe innovatief de ontwikkelaars zijn (hoeveel nieuwe Moon Craters worden er gevormd) en hoeveel de gamers (asteroïden) de huidige groepsgrootte waarderen bij het kiezen van welke groep ze willen deelnemen . Het blijkt dat gamers bij het kopen van games erg blind zijn voor groepen, maar precies het tegenovergestelde als ze ze spelen. Gaaf he?
Als je meer wilt weten over Zipf's Law en Power Law-distributies, is dit een leuke lezing. Kijk ook eens naar Newman's paper!
Als je meer van dit soort dingen wilt lezen, zal ik snel genoeg proberen om deze observatie bij een model te voegen, wat laat zien dat meer populaire multiplayer-spellen hogere prijzen hebben (die een link vormen naar de voorkeur van gamers om deel te nemen aan groepen van grotere omvang). Bekijk hier het artikel. Het Piece De Resistance-artikel zal proberen deze theorieën samen te voegen en uitleggen hoe games voor meerdere spelers, sociale netwerken en steden in feite allemaal anti-rivaliserende goederen met netwerkeffecten zijn (hoe meer mensen een goed consumeren, des te meer elke individuele consument er baat bij heeft) noemde hen deze Zipfische mist van mysterie ...
Tot dan - geniet ervan!
Postscriptum Voeg een opmerking toe met een leuk idee voor een 20/80-relatie waarvan je denkt dat die waar is.
De mijne zijn:
80% van de nostalgie van mensen wordt veroorzaakt door 20% van hun gelukkigste herinneringen (feitelijk bewezen voor de snelheid waarmee mensen informatie vergeten)
80% van de massa is geconcentreerd in 20% van de grootste ruimtevoorwerpen (feitelijk bewezen voor de verdeling van zwaartekracht)
En uiteraard
80% van de rommel in je toilet komt van 20% van wat je eet (geen academisch onderzoek om over te praten)